Với giải sách bài xích tập luyện Toán 8 Bài 11: Hình thang cân nặng sách Kết nối trí thức hoặc nhất, cụ thể sẽ hỗ trợ học viên dễ dàng và đơn giản thực hiện bài xích tập luyện vô SBT Toán 8 Bài 11.
Giải SBT Toán 8 Bài 11: Hình thang cân
Bạn đang xem: Sách bài tập Toán 8 Bài 11 (Kết nối tri thức): Hình thang cân | Giải SBT Toán lớp 8
Bài 3.7 trang 34 SBT Toán 8 Tập 1: Tính những góc của hình thang ABCD (AB, CD là nhì đáy) biết ,
Lời giải:
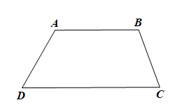
Trong hình thang ABCD có:
và là 2 góc bù nhau, và là 2 góc bù nhau.
Do đó ,
Mà nên , suy ra . Do đó
nên , hay , suy ra
Do đó
Vậy hình thang ABCD có
Bài 3.8 trang 34 SBT Toán 8 Tập 1: Chứng minh rằng vô hình thang có rất nhiều nhất nhì góc tù.
Lời giải:
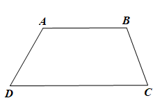
Xét hình thang ABCD sở hữu AB // CD
Ta có:
• và là nhì góc kề với cạnh mặt mũi AD
Suy ra nên vô nhì góc ê sở hữu đem quá 1 góc tù
• và là nhì góc kề với cạnh mặt mũi BC
Suy ra nên vô nhì góc ê sở hữu đem quá 1 góc tù
Do ê, vô tứ góc có tối đa 2 góc là góc tù.
Bài 3.9 trang 34 SBT Toán 8 Tập 1: Cho tam giác ABC vuông cân nặng bên trên đỉnh A. Ghép thêm nữa phía ngoài tam giác ê tam giác BCD vuông cân nặng bên trên đỉnh B. Chứng minh tứ giác ABDC là 1 hình thang vuông (hình thang sở hữu một cạnh mặt mũi vuông góc với nhì đáy).
Lời giải:
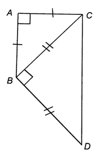
Do ∆ABC vuông cân nặng bên trên đỉnh A nên
Xét vô ∆ABC tớ có:
Nên
Do ∆BCD vuông cân nặng bên trên đỉnh B nên
Xét vô ∆BCD tớ có:
Nên
Ta có nên AB // CD (hai góc so sánh le vô vì thế nhau).
Vậy ABCD là 1 hình thang với AB, CD là nhì đáy; cạnh mặt mũi của hình thang này đó là AC vuông góc với lòng AB nên hình thang này đó là hình thang vuông.
Bài 3.10 trang 34 SBT Toán 8 Tập 1: Cho hình thang cân nặng ABCD với hai tuyến phố trực tiếp chứa chấp nhì cạnh mặt mũi AD, BC hạn chế nhau bên trên S. Gọi O là phó điểm của hai tuyến phố chéo cánh AC và BD. Chứng minh đường thẳng liền mạch SO trải qua trung điểm của AB, trải qua trung điểm của CD.
Lời giải:
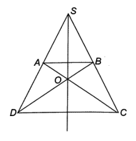
Xem thêm: Set Đồ SD214
Do ABCD là hình thang cân nặng nên AD = BC, AC = BD,
Xét ∆ABC và ∆BAD có
BC = AD, AC = BD, cạnh AB chung
Do ê ∆ABC = ∆BAD (c.c.c)
Suy ra .
Từ ê OAB là tam giác cân nặng bên trên O, nên OA = OB.
Ta có: OA + OC = AC; OB + OD = BD, tuy nhiên OA = OB, AC = BD
Suy rời khỏi OC = OD.
Do ê O cơ hội đều A và B; O cơ hội đều C và D;
Do AB // CD nên ; (các cặp góc ở địa điểm đồng vị)
Mà hay suy ra
Suy rời khỏi SAB, SCD là những tam giác cân nặng bên trên đỉnh S nên SA = SB, SC = SD
Do ê S cũng cơ hội đều A và B, cơ hội đều C và D.
Vậy S và O nằm trong phía trên đàng trung trực của AB, của CD nên đường thẳng liền mạch SO trải qua trung điểm của AB, CD.
Bài 3.11 trang 34 SBT Toán 8 Tập 1: Cho hình thang cân nặng ABCD với nhì lòng AB và CD, đàng chéo cánh AC vuông góc với cạnh mặt mũi AD, tia CA là tia phân giác của góc C. Tính chu vi của hình thang ê hiểu được AD = 2 centimet.
Lời giải:
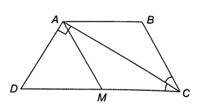
Do CA là tia phân giác của nên
Mà ABCD là hình thang cân nặng nên AB // CD, suy ra (hai góc so sánh le trong)
Do ê, , suy rời khỏi ∆ABC cân nặng bên trên B.
Đặt thì .
Vì ABCD là hình thang cân nặng nên
Tam giác ADC vuông bên trên A nên suy ra
Lấy điểm M nằm trong cạnh huyền DC sao mang lại DM = AD, mà thì AMD là tam giác đều, nên
Khi đó
Suy ra nên tam giác MAC cân nặng bên trên M
Do ê AM = MC, tuy nhiên AM = DM = AD
Nên AM = DM = AD = MC hoặc DC = 2AD.
Vậy AB = BC = AD, DC = 2AD nên chu vi hình thang bằng
AB + BC + CD + AD = 5AD = 5.2 = 10 centimet.
Xem tăng Lời giải bài tập luyện SBT Toán 8 Kết nối tri thức hoặc, cụ thể khác:
Bài 10: Tứ giác
Bài 12: Hình bình hành
Xem thêm: Tổng hợp toàn bộ giải thưởng tại The Game Award 2023: Game of the Year gọi tên Baldur's Gate 3
Bài 13: Hình chữ nhật
Bài 14: Hình thoi và hình vuông
Bài tập luyện cuối chương 3